Duration is a measure of the average (cash-weighted) term-to-maturity of a bond. In plain-terms – think of it as an approximation of how long it will take to recoup your initial investment in the bond.
There are two types of duration: Macaulay duration and modified duration. Macaulay duration is useful in immunization, where a portfolio of bonds is constructed to fund a known liability. Modified duration is an extension of Macaulay duration and is a useful measure of the sensitivity of a bond’s price (the present value of its cash flows) to interest rate movements.
Macaulay Duration
The calculation of Macaulay Duration is shown below:
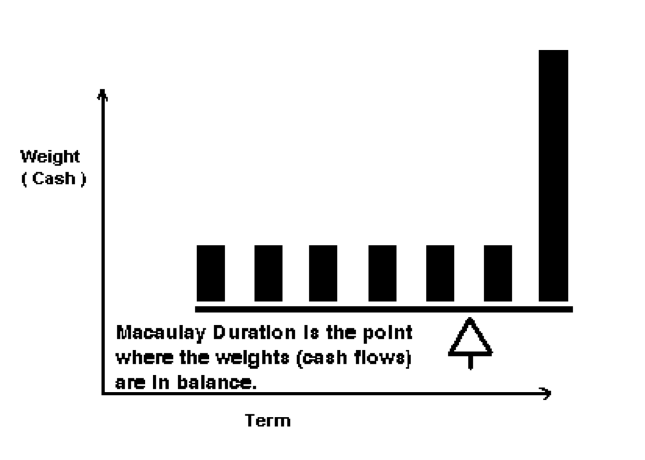
Graphically, Macaulay Duration is the point of balance (in years) for the cash flows from the bond (see below).
Modified Duration
Modified duration is a measure of the price sensitivity of a bond to interest rate movements. It is calculated as shown below:
Modified Duration = Macaulay Duration /( 1 + y/n), where y = yield to maturity and n = number of discounting periods in year ( 2 for semi – annual paying bonds )
Then, % Price Change = -1 * Modified Duration * Yield Change
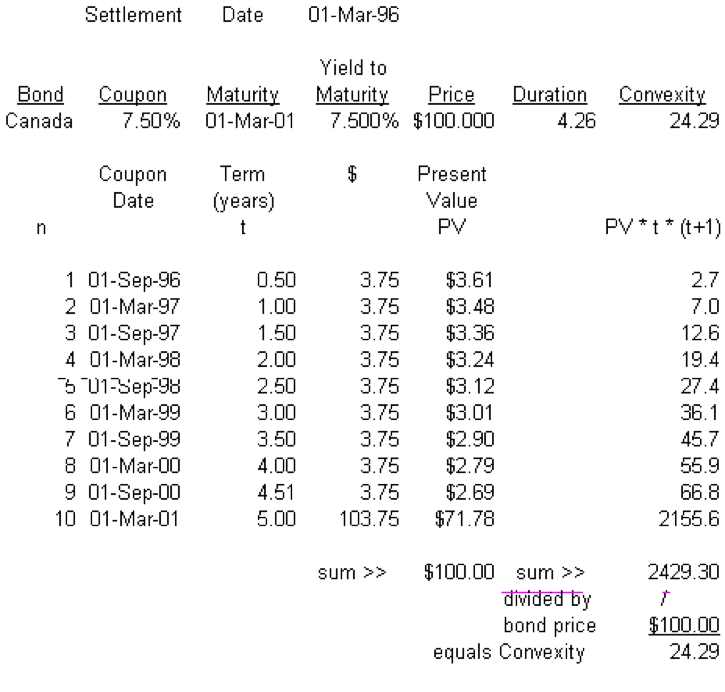
Modified duration indicates the percentage change in the price of a bond for a given change in yield. The percentage change applies to the price of the bond including accrued interest. In the section showing a bond’s price as the present value of its cash flows, the bond shown was priced initially at par (100), when the YTM was 7.5%, with a Macaulay Duration of 4.26 years. The bond was repriced for an increase and decrease in rates of 2.5%. The Modified Duration for this bond will be: Dmod = -1 * 4.26 / (1 + .075/2) = 4.106 years. Therefore, a change in the yield of +/- 2.5% should result in a percentage change in the price of the bond of: -/+ 4.106 * .025 = +/- 0.10265 (+/- 10.265 %). Since the bond was initially priced at par, the estimated prices are: $110.27 at 5.00% and $89.74 at 10.00%. The actual prices were: $110.94 at 5.00% and $90.35 at 10.00%. The discrepancy between the estimated change in the bond price and the actual change is due to the convexity of the bond, which must be included in the price change calculation when the yield change is large. However, modified duration is still a good indication of the potential price volatility of a bond.

Convexity
The previous percentage price change calculation was inaccurate because it failed to account for the convexity of the bond (the curvature in the above picture). An easy way to think of convexity is that convexity is the rate of change of duration with yield, and accounts for the fact that as the yield decreases, the slope of the price – yield curve, and duration, will increase. Similarly, as the yield increases, the slope of the curve will decrease, as will the duration. Convexity is a measure of the amount of “whip” in the bond’s price yield curve (see above) and is so named because of the convex shape of the curve. Because of the shape of the price yield curve, for a given change in yield down or up, the gain in price for a drop in yield will be greater than the fall in price due to an equal rise in yields. This slight “upside capture, downside protection” is what convexity accounts for. Mathematically ‘Dmod’ is the first derivative of price with respect to yield and convexity is the second derivative of price with respect to yield. Another way to view it is, convexity is the first derivative of modified duration. By using convexity in the yield change calculation, a much closer approximation is achieved (an exact calculation would require many more terms and is not useful).
Using convexity (C) and Dmod then: % Price Chg. = -1 * D mod * Yield Chg. + C/2 * Yield Chg * Yield Chg.
Using the previous example, convexity can be calculated and results in the expected price change being: $111.02 at 5.00% and $90.49 at 10.00% The actual prices were: $110.94 at 5.00% and $90.35 at 10.00%
In summary, Macauley duration is a weighted average maturity of cash flows (measured in units of time) and is useful in portfolio immunization where a portfolio of bonds is used to fund a known liability. Modified duration is a price sensitivity measure and is the percentage change in price for a unit change in yield. Modified duration is more commonly used than Macauley duration and is a tool that provides an approximate measure of how a bond price will change given a modest change in yield. For larger changes in yield, both the modified duration and convexity are used to better approximate how a bond price will change for a given change in yield.